Introduction to LangChain
What is LangChain?
LangChain is a framework for building applications powered by large language models. Developers believe the most powerful, differentiated apps will not just call language models but also have:
- Data awareness: Connect language models with other data sources
- Agency: Allow language models to interact with environments
LangChain supports Python and JavaScript. It focuses on composability and modularity.
Official docs: https://python.langchain.com/en/latest/
LangChain's Modularity
Includes many integrated conversational and chat models; prompt templates, output parsers, example selectors.
Supports retrieving and calling other data sources including but not limited to text, arrays. Supports multiple data retrieval tools.
Supports building conversational chain templates to automatically generate standardized outputs based on inputs.
Can call multiple preset or custom algorithms and utilities.
Models, Prompts and Output Parsers
Prompt Templates
We typically call GPT like this:
import os
import openai
from dotenv import load_dotenv, find_dotenv
_ = load_dotenv(find_dotenv()) # read local .env file
openai.api_key = os.environ['OPENAI_API_KEY']
def get_completion(prompt, model="gpt-3.5-turbo"):
messages = [{"role": "user", "content": prompt}]
response = openai.ChatCompletion.create(
model=model,
messages=messages,
temperature=0,
)
return response.choices[0].message["content"]
# Create a call function
prompt = f"""Translate the text
that is delimited by triple backticks
into a style that is {style}.
text: ```{customer_email}```
"""
# Write the prompt
response = get_completion(prompt)
# Generate result
Now see how Langchain calls models:
from langchain.chat_models import ChatOpenAI
llm_model="gpt-3.5-turbo"
chat = ChatOpenAI(temperature=0.0, model="llm_model")
# Load langchain chat model, set randomness to 0
template_string = """Translate the text
that is delimited by triple backticks
into a style that is {style}.
text: ```{text}```
"""
# Design template info
from langchain.prompts import ChatPromptTemplate
prompt_template = ChatPromptTemplate.from_template(template_string)
# Load prompt template, load template info
customer_style = """American English
in a calm and respectful tone
"""
customer_email = """
Arrr, I be fuming that me blender lid
flew off and splattered me kitchen walls
with smoothie! And to make matters worse,
the warranty don't cover the cost of
cleaning up me kitchen. I need yer help
right now, matey!
"""
# Define variable fields in template
customer_messages = prompt_template.format_messages(
style=customer_style,
text=customer_email)
# Call template, assign values to variables, generate final prompt
customer_response = chat(customer_messages)
#print(type(customer_messages))
#print(type(customer_messages[0]))
#print(customer_messages[0]) content="Translate the text that is delimited by triple backticks into a style that is American English in a calm and respectful tone\n. text: ```\nArrr, I be fuming that me blender lid flew off and splattered me kitchen walls with smoothie! And to make matters worse, the warranty don't cover the cost of cleaning up me kitchen. I need yer help right now, matey!\n```\n" additional_kwargs={} example=False
#AIMessage(content="I'm really frustrated that my blender lid flew off and made a mess of my kitchen walls with smoothie. To add to my frustration, the warranty doesn't cover the cost of cleaning up my kitchen. Can you please help me out, friend?", additional_kwargs={}, example=False)
# Call prompt, generate result
By "creating a prompt template with variables", we can flexibly generate new prompts by changing variable info. This allows template reuse.
Output Parsers
Convert language model outputs into specific structured outputs like dicts, arrays, etc.
from langchain.output_parsers import ResponseSchema
from langchain.output_parsers import StructuredOutputParser
# Load output parsers
gift_schema = ResponseSchema(name="gift",
description="Was the item purchased\
as a gift for someone else? \
Answer True if yes,\
False if not or unknown.")
delivery_days_schema = ResponseSchema(name="delivery_days",
description="How many days\
did it take for the product\
to arrive? If this \
information is not found,\
output -1.")
price_value_schema = ResponseSchema(name="price_value",
description="Extract any\
sentences about the value or \
price, and output them as a \
comma separated Python list.")
response_schemas = [gift_schema,
delivery_days_schema,
price_value_schema]
# Create parse rules
output_parser = StructuredOutputParser.from_response_schemas(response_schemas)
format_instructions = output_parser.get_format_instructions()
# Compile parse rules
review_template_2 = """
For the following text, extract the following information:
gift: Was the item purchased as a gift for someone else?
Answer True if yes, False if not or unknown.
delivery_days: How many days did it take for the product
to arrive? If this information is not found, output -1.
price_value: Extract any sentences about the value or price,
and output them as a comma separated Python list.
text: {text}
{format_instructions}
"""
# Create a prompt template, add compiled parse rules
prompt = ChatPromptTemplate.from_template(template=review_template_2)
messages = prompt.format_messages(text=customer_review,
format_instructions=format_instructions)
# Generate prompt info through template
response = chat(messages)
# Generate result
output_dict = output_parser.parse(response.content)
# Save result to dict
Memory Components
Large language models do not automatically remember conversation history/context when called through APIs. Langchain's memory components provide various ways to remember conversation history/context.
Outline
- ConversationBufferMemory
- ConversationBufferWindowMemory
- ConversationTokenBufferMemory
- ConversationSummaryMemory
ConversationBufferMemory
from langchain.chat_models import ChatOpenAI
from langchain.chains import ConversationChain
from langchain.memory import ConversationBufferMemory
# Load required packages
llm = ChatOpenAI(temperature=0.0)
memory = ConversationBufferMemory()
conversation = ConversationChain(
llm=llm,
memory = memory,
verbose=True
)
# Create a conversation, context store, conversational chain.
conversation.predict(input="Hi, my name is Andrew")
conversation.predict(input="What is 1+1?")
conversation.predict(input="What is my name?")
# Add convo content, questions and answers are saved to context store
print(memory.buffer)
memory.load_memory_variables({})
# Display convo content saved in context store
memory.save_context({"input": "Hi"},
{"output": "What's up"})
# Directly assign QA pairs to context store
ConversationBufferWindowMemory
from langchain.memory import ConversationBufferWindowMemory
# Load component
memory = ConversationBufferWindowMemory(k=1)
# Add a memory store with only 1 slot
memory.save_context({"input": "Hi"},
{"output": "What's up"})
memory.save_context({"input": "Not much, just hanging"},
{"output": "Cool"})
# In this case, program only remembers the latest 1 QA pair in the 1 slot store.
ConversationTokenBufferMemory
from langchain.memory import ConversationTokenBufferMemory
from langchain.llms import OpenAI
llm = ChatOpenAI(temperature=0.0)
# Load components
memory = ConversationTokenBufferMemory(llm=llm, max_token_limit=30)
# Create a 30 token memory store (needs LLM for limited space judgment)
memory.save_context({"input": "AI is what?!"},
{"output": "Amazing!"})
memory.save_context({"input": "Backpropagation is what?"},
{"output": "Beautiful!"})
memory.save_context({"input": "Chatbots are what?"},
{"output": "Charming!"})
# In this case, program only remembers latest QA pairs under 30 tokens.
# It's fine if only answers exist without questions.
memory.load_memory_variables({})
# Show result: {'history': 'AI: Beautiful!\nHuman: Chatbots are what?\nAI: Charming!'}
ConversationSummaryMemory
from langchain.memory import ConversationSummaryBufferMemory
# Load package
schedule = """There is a meeting at 8am with your product team.
You will need your powerpoint presentation prepared.
9am-12pm have time to work on your LangChain
project which will go quickly because Langchain is such a powerful tool.
At Noon, lunch at the italian resturant with a customer who is driving
from over an hour away to meet you to understand the latest in AI.
Be sure to bring your laptop to show the latest LLM demo."
# A long content
memory = ConversationSummaryBufferMemory(llm=llm, max_token_limit=100)
# Create a 100 token conversational summary memory (needs LLM for summarization)
memory.save_context({"input": "Hello"}, {"output": "What's up"})
memory.save_context({"input": "Not much, just hanging"},
{"output": "Cool"})
memory.save_context({"input": "What is on the schedule today?"},
{"output": f"{schedule}"})
# Add convos
memory.load_memory_variables({})
# Show summarized result under 100 tokens: {'history': "System: The human and AI engage in small talk before discussing the day's schedule. The AI informs the human of a morning meeting with the product team, time to work on the LangChain project, and a lunch meeting with a customer interested in the latest AI developments."}
conversation = ConversationChain(
llm=llm,
memory = memory,
verbose=True
)
conversation.predict(input="What would be a good demo to show?")
# Specifically, when calling summary memory in convo, the latest AI response will be saved verbatim (not summarized).
# Other convo content will be summarized. This may be to better get good answers without losing key info from latest AI response.
Chains
Outline
- LLMChain
- Sequential Chains
- SimpleSequentialChain
- SequentialChain
- Router Chain
LLMChain
from langchain.chat_models import ChatOpenAI
from langchain.prompts import ChatPromptTemplate
from langchain.chains import LLMChain
llm = ChatOpenAI(temperature=0.9)
# Load packages
prompt = ChatPromptTemplate.from_template(
"What is the best name to describe
a company that makes {product}?"
)
# Create a prompt template with variable {product}
chain = LLMChain(llm=llm, prompt=prompt)
# Create a basic chat chain
product = "Queen Size Sheet Set"
chain.run(product)
# Assign variable, get answer
SimpleSequentialChain
General sequential chains can pass the output of one chain as input to the next chain. Simple sequential chains have a single input and output variable.
from langchain.chains import SimpleSequentialChain
llm = ChatOpenAI(temperature=0.9)
# Load packages
first_prompt = ChatPromptTemplate.from_template(
"What is the best name to describe
a company that makes {product}?"
)
# Prompt template 1, variable is {product}
chain_one = LLMChain(llm=llm, prompt=first_prompt)
# Chain 1
second_prompt = ChatPromptTemplate.from_template(
"Write a 20 words description for the following
company:{company_name}"
)
# Prompt template 2, variable is {company_name}
chain_two = LLMChain(llm=llm, prompt=second_prompt)
# Chain 2
overall_simple_chain = SimpleSequentialChain(chains=[chain_one, chain_two],
verbose=True)
overall_simple_chain.run(product)
"""
> Entering new SimpleSequentialChain chain...
Royal Sheets Co.
Royal Sheets Co. is the premium manufacturer and supplier of luxurious bedding essentials, offering a variety of high-quality sheets, pillowcases, and more.
> Finished chain.
'Royal Sheets Co. is the premium manufacturer and supplier of luxurious bedding essentials, offering a variety of high-quality sheets, pillowcases, and more.'
"""
# Combine chain 1 and 2, get result
SequentialChain
Sequential chains contain multiple chains where some chain outputs can be inputs to other chains. Sequential chains can support multiple input and output variables.
from langchain.chains import SequentialChain
llm = ChatOpenAI(temperature=0.9)
# Load
first_prompt = ChatPromptTemplate.from_template(
"Translate the following review to english:"
"\n\n{Review}"
)
chain_one = LLMChain(llm=llm, prompt=first_prompt,
output_key="English_Review"
)
# Chain 1: input Review, output English_Review
second_prompt = ChatPromptTemplate.from_template(
"Can you summarize the following review in 1 sentence:"
"\n\n{English_Review}"
)
chain_two = LLMChain(llm=llm, prompt=second_prompt,
output_key="summary"
)
# Chain 2: input English_Review, output summary
third_prompt = ChatPromptTemplate.from_template(
"What language is the following review:\n\n{Review}"
)
chain_three = LLMChain(llm=llm, prompt=third_prompt,
output_key="language"
)
# Chain 3: input Review, output language
fourth_prompt = ChatPromptTemplate.from_template(
"Write a follow up response to the following "
"summary in the specified language:"
"\n\nSummary: {summary}\n\nLanguage: {language}"
)
chain_four = LLMChain(llm=llm, prompt=fourth_prompt,
output_key="followup_message"
)
# Chain 4: input summary, language, output followup_message
overall_chain = SequentialChain(
chains=[chain_one, chain_two, chain_three, chain_four],
input_variables=["Review"],
output_variables=["English_Review", "summary","followup_message"],
verbose=True
)
# Build full chain, input Review, output "English_Review", "summary","followup_message"
overall_chain(review)
"""
> Entering new SequentialChain chain...
> Finished chain.
{'Review': "Je trouve le goût médiocre. La mousse ne tient pas, c'est bizarre. J'achète les mêmes dans le commerce et le goût est bien meilleur...\nVieux lot ou contrefaçon !?",
'English_Review': "I find the taste mediocre. The foam doesn't hold up, it's weird. I buy the same ones at the store and the taste is much better... Old batch or counterfeit!?",
'summary': 'The reviewer is dissatisfied with the taste and foam quality of the product bought online, suggesting that it may be an old batch or counterfeit.',
'followup_message': "Réponse de suivi:\n\nNous sommes désolés d'apprendre que vous n'êtes pas satisfait de la qualité du produit que vous avez acheté en ligne. Nous prenons cela très au sérieux et nous aimerions proposer notre aide pour trouver une solution. Pouvez-vous nous envoyer des photos de l'emballage et du produit lui-même? Cela nous aidera à déterminer s'il s'agit effectivement d'un ancien lot ou d'un produit contrefait. Nous sommes heureux de remplacer le produit ou de vous offrir un remboursement complet si nécessaire. Nous espérons que cela résoudra le problème et que vous serez satisfait de l'expérience client avec notre entreprise."}
"""
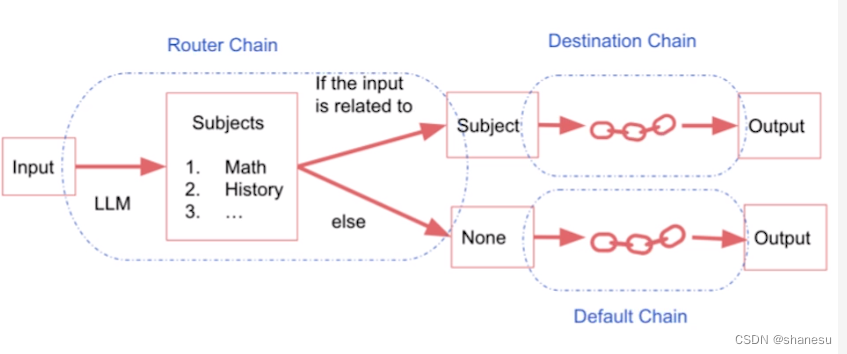
Router Chain
Router chains are like while-else functions that route inputs to different subsequent chain paths based on criteria. A router chain normally has one input and one output.
physics_template = """You are a very smart physics professor.
You are great at answering questions about physics in a concise
and easy to understand manner.
When you don't know the answer to a question you admit
that you don't know.
Here is a question:
{input}"""
math_template = """You are a very good mathematician.
You are great at answering math questions.
You are so good because you are able to break down
hard problems into their component parts,
answer the component parts, and then put them together
to answer the broader question.
Here is a question:
{input}"""
history_template = """You are a very good historian.
You have an excellent knowledge of and understanding of people,
events and contexts from a range of historical periods.
You have the ability to think, reflect, debate, discuss and
evaluate the past. You have a respect for historical evidence
and the ability to make use of it to support your explanations
and judgements.
Here is a question:
{input}"""
computerscience_template = """ You are a successful computer scientist.
You have a passion for creativity, collaboration,
forward-thinking, confidence, strong problem-solving capabilities,
understanding of theories and algorithms, and excellent communication
skills. You are great at answering coding questions.
You are so good because you know how to solve a problem by
describing the solution in imperative steps
that a machine can easily interpret and you know how to
choose a solution that has a good balance between
time complexity and space complexity.
Here is a question:
{input}"""
# Create 4 prompt templates
prompt_infos = [
{
"name": "physics",
"description": "Good for answering questions about physics",
"prompt_template": physics_template
},
{
"name": "math",
"description": "Good for answering math questions",
"prompt_template": math_template
},
{
"name": "History",
"description": "Good for answering history questions",
"prompt_template": history_template
},
{
"name": "computer science",
"description": "Good for answering computer science questions",
"prompt_template": computerscience_template
}
]
# Prompt template info
from langchain.chains.router import MultiPromptChain
from langchain.chains.router.llm_router import LLMRouterChain,RouterOutputParser
from langchain.prompts import PromptTemplate
llm = ChatOpenAI(temperature=0)
# Load
destination_chains = {}
for p_info in prompt_infos:
name = p_info["name"]
prompt_template = p_info["prompt_template"]
prompt = ChatPromptTemplate.from_template(template=prompt_template)
chain = LLMChain(llm=llm, prompt=prompt)
destination_chains[name] = chain
destinations = [f"{p['name']}: {p['description']}" for p in prompt_infos]
destinations_str = "\n".join(destinations)
# Generate 4 chains based on template info, save to destination
default_prompt = ChatPromptTemplate.from_template("{input}")
LangChain: Q&A over Documents
LangChain has retrieval capabilities to answer questions by searching through documents provided by the user. Here is how it works:
How it Works
- At preprocessing time, the document contents (e.g. a list) are split into multiple chunks.
- The chunks are embedded into vector representations using embed techniques.
- At question time, the question is also embedded into a vector representation.
- The question vector is compared to the document chunk vectors to find the most similar chunks.
- At answer time, the relevant chunks are fed into a large language model to generate the final response.
Implementation 1: Retrieve from CSV
from langchain.chains import RetrievalQA
from langchain.chat_models import ChatOpenAI
from langchain.document_loaders import CSVLoader
from langchain.vectorstores import DocArrayInMemorySearch
from IPython.display import display, Markdown
# Load packages
file = 'OutdoorClothingCatalog_1000.csv'
loader = CSVLoader(file_path=file)
# Load file
from langchain.indexes import VectorstoreIndexCreator
index = VectorstoreIndexCreator(
vectorstore_cls=DocArrayInMemorySearch
).from_loaders([loader])
# Create vector index from CSV
query = "Please list all your shirts with sun protection in a table in markdown and summarize each one."
response = index.query(query)
display(Markdown(response))
# Ask a question and display markdown response
Implementation 2: Retrieve from Documents
# Embed question
from langchain.embeddings import OpenAIEmbeddings
embeddings = OpenAIEmbeddings()
embed = embeddings.embed_query("Hi my name is Harrison")
# Embed and index documents
from langchain.vectorstores import DocArrayInMemorySearch
db = DocArrayInMemorySearch.from_documents(
docs,
embeddings
)
# Find similar documents
query = "Please suggest a shirt with sunblocking"
docs = db.similarity_search(query)
# Pass to LLM with question
from langchain.chat_models import ChatOpenAI
llm = ChatOpenAI(temperature = 0.0)
qdocs = "".join([docs[i].page_content for i in range(len(docs))])
response = llm(f"{qdocs} Question: Please list all your shirts with sun protection in a table in markdown and summarize each one.")
# Display markdown response
display(Markdown(response))
Built-in Retrievers
from langchain.chains import RetrievalQA
from langchain.chat_models import ChatOpenAI
from langchain.document_loaders import CSVLoader
from langchain.indexes import StuffIndex
# Load docs
docs = # Load from CSV
# Index documents
index = StuffIndex(docs)
# Create retriever
retriever = index.retriever()
# Initialize chain
qa = RetrievalQA(retriever=retriever, llm=llm)
# Ask question
response = qa("What shirts have sun protection?")
Evaluation
LangChain can generate QA examples for a given document, or evaluate existing QAs.
Outline
- Generate examples
- Manual evaluation
- LLM-assisted evaluation
Generate Examples
from langchain.evaluation.qa import QAGenerateChain
# Create example generator
example_gen_chain = QAGenerateChain.from_llm(ChatOpenAI())
# Apply to docs
new_examples = example_gen_chain.apply_and_parse(
[{"doc": t} for t in data[:5]]
)
Manual Evaluation
import langchain
langchain.debug = True
qa.run(examples[0]["query"])
langchain.debug = False
LLM-assisted Evaluation
# Generate predictions
predictions = qa.apply(examples)
from langchain.evaluation.qa import QAEvalChain
llm = ChatOpenAI(temperature=0)
eval_chain = QAEvalChain.from_llm(llm)
# Evaluate
graded_outputs = eval_chain.evaluate(examples, predictions)
# Print evaluations
for i, eg in enumerate(examples):
print(f"Example {i}:")
print("Question: " + predictions[i]['query'])
print("Real Answer: " + predictions[i]['answer'])
print("Predicted Answer: " + predictions[i]['result'])
print("Predicted Grade: " + graded_outputs[i]['text'])
print()
'''
Example 0:
Question: Do the Cozy Comfort Pullover Set have side pockets?
Real Answer: Yes
Predicted Answer: The Cozy Comfort Pullover Set, Stripe has side pockets on the pull-on pants.
Predicted Grade: CORRECT
Example 1:
Question: What collection is the Ultra-Lofty 850 Stretch Down Hooded Jacket from?
Real Answer: The DownTek collection
Predicted Answer: The Ultra-Lofty 850 Stretch Down Hooded Jacket is from the DownTek collection.
Predicted Grade: CORRECT
Example 2:
Question: What is the approximate weight of the Women's Campside Oxfords per pair?
Real Answer: The approximate weight of the Women's Campside Oxfords per pair is 1 lb.1 oz.
Predicted Answer: The approximate weight of the Women's Campside Oxfords per pair is 1 lb. 1 oz.
Predicted Grade: CORRECT
Example 3:
Question: What is the construction material of the Recycled Waterhog Dog Mat?
Real Answer: The Recycled Waterhog Dog Mat is constructed from 24 oz. polyester fabric made from 94% recycled materials with a rubber backing.
Predicted Answer: The Recycled Waterhog Dog Mat is constructed with a 24 oz. polyester fabric made from 94% recycled materials and a rubber backing.
Predicted Grade: CORRECT
Example 4:
Question: What are the features of the Infant and Toddler Girls' Coastal Chill Swimsuit, Two-Piece?
Real Answer: The swimsuit features bright colors, ruffles, and exclusive whimsical prints. It is made of four-way-stretch and chlorine-resistant fabric that keeps its shape and resists snags. The swimsuit is UPF 50+ rated, providing the highest rated sun protection possible by blocking 98% of the sun's harmful rays. It has crossover no-slip straps and a fully lined bottom for a secure fit and maximum coverage. The swimsuit can be machine washed and line dried for best results.
Predicted Answer: The Infant and Toddler Girls' Coastal Chill Swimsuit, Two-Piece features bright colors, ruffles, and exclusive whimsical prints. The four-way-stretch and chlorine-resistant fabric keeps its shape and resists snags. The UPF 50+ rated fabric provides the highest rated sun protection possible, blocking 98% of the sun's harmful rays. The crossover no-slip straps and fully lined bottom ensure a secure fit and maximum coverage. It is machine washable and should be line dried for best results. It is imported.
Predicted Grade: CORRECT
Example 5:
Question: What is the fabric composition of the swimtop and what is its sun protection rating?
Real Answer: The swimtop is made of 82% recycled nylon with 18% Lycra® spandex, and is lined with 90% recycled nylon with 10% Lycra® spandex. It has a UPF 50+ rating, which is the highest rated sun protection possible.
Predicted Answer: The swim top is made of 80% nylon and 20% Lycra Xtra Life fiber. It has a UPF 50+ rating, which is the highest rated sun protection possible. The high-performance fabric also blocks 98% of the sun's harmful rays and is recommended by The Skin Cancer Foundation as an effective UV protectant.
Predicted Grade: CORRECT
Example 6:
Question: What is the name of the pants and what technology makes them more breathable?
Real Answer: The pants are named EcoFlex 3L Storm Pants and the TEK O2 technology makes them more breathable.
Predicted Answer: The name of the pants is EcoFlex 3L Storm Pants. The technology that makes them more breathable is TEK O2 technology.
Predicted Grade: CORRECT
'''
graded_outputs[0]
# {'text': 'CORRECT'}
Agents
LLMs alone cannot answer knowledge questions well since their knowledge is compressed. Agents act like an assistant that can use tools and information to help answer questions.
Outline
- Using built-in tools like search and Wikipedia
- Defining custom tools
Built-in Tools
from langchain.agents.agent_toolkits import create_python_agent
from langchain.agents import load_tools, initialize_agent
from langchain.agents import AgentType
from langchain.tools.python.tool import PythonREPLTool
from langchain.python import PythonREPL
from langchain.chat_models import ChatOpenAI
# Load packages
llm = ChatOpenAI(temperature=0)
tools = load_tools(["llm-math","wikipedia"], llm=llm)
# Load tools
agent= initialize_agent(
tools,
llm,
agent=AgentType.CHAT_ZERO_SHOT_REACT_DESCRIPTION,
handle_parsing_errors=True,
verbose = True)
# Initialize agent
agent("What is the 25% of 300?")
# Use math tool
question = "Tom M. Mitchell is an American computer scientist and the Founders University Professor at Carnegie Mellon University (CMU) what book did he write?"
result = agent(question)
# Use Wikipedia tool
Python Agent
from langchain.agents.agent_toolkits import create_python_agent
from langchain.python import PythonREPL
agent = create_python_agent(
llm,
tool=PythonREPLTool(),
verbose=True
)
# Create Python agent
customer_list = [["Harrison", "Chase"],
["Lang", "Chain"],
["Dolly", "Too"],
["Elle", "Elem"],
["Geoff","Fusion"],
["Trance","Former"],
["Jen","Ayai"]]
agent.run(f"""Sort these customers by last name and then first name and print the output: {customer_list}""")
# Use Python sorted()
Custom Tools
from langchain.agents import tool
from datetime import date
@tool
def time(text: str) -> str:
"""Returns todays date, use this for any questions related to knowing todays date. The input should always be an empty string, and this function will always return todays date - any date mathmatics should occur outside this function."""
return str(date.today())
# Define custom tool
agent= initialize_agent(
tools + [time],
llm,
# Add tool to agent
)
try:
result = agent("whats the date today?")
except:
print("exception on external access")
# Use custom tool
This allows the agent to leverage tools automatically to assist in answering questions.








