Summary:
- This paper introduces a variant of LSTM which can unsupervisely learn latent sentences structures(?), further benefiting grammar related tasks(unsupervised constituency parsing, target syntactic evaluation, etc.)
- It introduces two additional gates: Master Forget Gate and Master Input Gate controlling updating mechanism of LSTM
- It divides hidden state into an unequal place: higher location(those with bigger indexes) are used for storing history information and harder to erase, lower locations are for newer information. The division is not hard(by binary gates I mean), but by softmax gates for back propagating purpose.
Overall Designing Principles
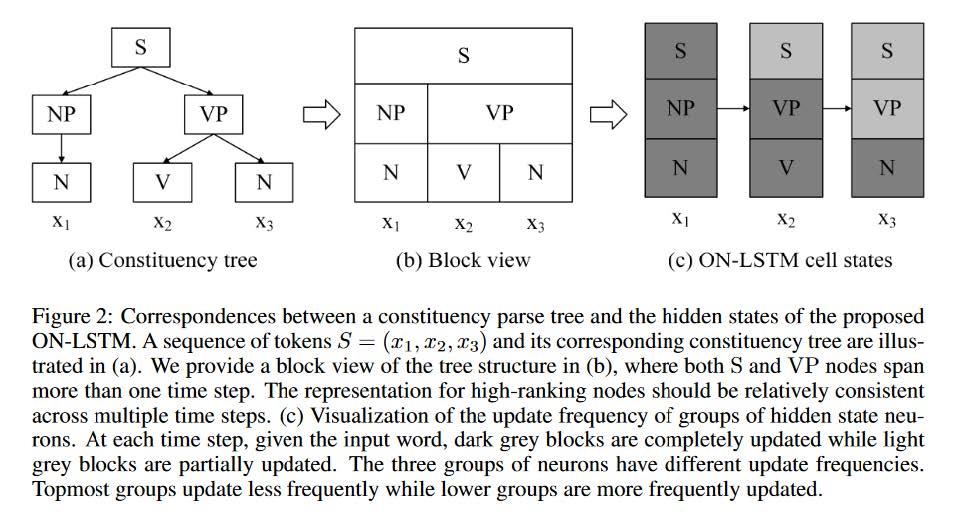
- Languages are hierarchical and structured.
And the author wants to incorporate this prior to the model. For each time step t. Some parts of the hidden states should be preserved(correspond to top layers in the hierarchy, like the S which stands for subject in the figure. This of course should be kept further.)
To this end, Master Forget Gate and Master Input Gate controlling updating mechanism of LSTM have been proposed.
We wan to define $d^f_t$ and $d_t^i$ which represent the split points for
(0,...,0, 1,...,1) (idealized Master Forget Gate)and
(1, ..., 1, 0, ..,0, 0) (idealized Master Input Gate)respectively.
Consider two different cases:
Case I: $d^f_t \le d_t^i$, input level $d_t^i$ is greater or equal to forget(history) level $d^f_t$ .
0 0 0 1 1 1 1 1 $d^f_t=4$
1 1 1 1 0 0 0 0 $d_t^i=4$
N N N C O O O O
Where N means update with new element, C means standard LSTM update meachanism, O stands for keep original information.
Case II: $d^f_t \gt d_t^i$, input level $d_t^i$ is less than forget(history) level $d^f_t$ .
0 0 0 0 1 1 1 1 $d^f_t=5$
1 1 1 0 0 0 0 0 $d_t^i=3$
N N N X O O O O
Where X means putting 0 in that position.
But outputing binary is differentiable in neural nets, so author chooses softmaxen-ed operations instead.
Define operation cumax :
def cumsoftmax(x, dim=-1):
return torch.cumsum(F.softmax(x, dim=dim), dim=dim)
Define Master Forget Gate and Master Input Gate as:
$$\begin{array}{l}
\tilde{f}_{t}=\overrightarrow{\mathrm{cumsum}}\left(\operatorname{softmax}\left(W_{\dot{f}} x_{t}+U_{\tilde{f}} h_{t-1}+b_{\tilde{f}}\right)\right) \\
\tilde{i}_{t}=\overleftarrow{\mathrm{cumsum}}\left(\operatorname{softmax}\left(W_{\tilde{i}} x_{t}+U_{\tilde{i}} h_{t-1}+b_{\tilde{i}}\right)\right) =1-
\overrightarrow{\mathrm{cumsum}}\left(\operatorname{softmax}\left(W_{\tilde{i}} x_{t}+U_{\tilde{i}} h_{t-1}+b_{\tilde{i}}\right)\right)
\end{array}$$
Comparison to LSTM
Note:
- Blue stands for Gate Mechanism (LSTM)
- Red stands for content updating mechanism (LSTM)
- Fuchsia stands for ON-LSTM introduced Gate Mechanism (ON-LSTM)
- Green stands for ON-LSTM impacted Gates (ON-LSTM)
- This yellowish #e69138 color stands for impacted content updating mechanism (ON-LSTM)
LSTM:
Forget gate: controls what is kept vs forgotten, from previous cell state
$\boldsymbol{f}^{(t)}=\sigma \left(\boldsymbol{W}_{f} \boldsymbol{h}^{(t-1)}+\boldsymbol{U}_{f} \boldsymbol{x}^{(t)}+\boldsymbol{b}_{f}\right)$
Input gate: controls what parts of the new cell content are written to cell
$\boldsymbol{i}^{(t)}=\sigma \left(\boldsymbol{W}_{i} \boldsymbol{h}^{(t-1)}+\boldsymbol{U}_{i} \boldsymbol{x}^{(t)}+\boldsymbol{b}_{i}\right)$
Output gate: controls what parts of cell are output to hidden state
$\boldsymbol{o}^{(t)}=\sigma \left(\boldsymbol{W}_{o} \boldsymbol{h}^{(t-1)}+\boldsymbol{U}_{o} \boldsymbol{x}^{(t)}+\boldsymbol{b}_{o}\right)$
New cell content: this is the new content to be written to the cell
$\tilde{\boldsymbol{c}}^{(t)}=\tanh \left(\boldsymbol{W}_{c} \boldsymbol{h}^{(t-1)}+\boldsymbol{U}_{c} \boldsymbol{x}^{(t)}+\boldsymbol{b}_{c}\right)$
Cell state: erase (“forget”) some content from last cell state, and write (“input”) some new cell content
$\boldsymbol{c}^{(t)}=\boldsymbol{f}^{(t)} \circ \boldsymbol{c}^{(t-1)}+\boldsymbol{i}^{(t)} \circ \tilde{\boldsymbol{c}}^{(t)}$
Hidden state: read (“output”) some content from the cell
$\boldsymbol{h}^{(t)}=\boldsymbol{o}^{(t)} \circ \tanh \boldsymbol{c}^{(t)}$
 |
| LSTM, Source: https://kexue.fm/archives/6621 |
ON-LSTM
Intersection(Optional): Hadamard Product between Master Forget Gate and Master Input Gate
$\omega_t= \tilde{f_t} \cdot \tilde{i_t}$
$\omega_t= \tilde{f_t} \cdot \tilde{i_t}$
Master Forget gate: Ordered Forget Gate Control Mechanism
$\tilde{f}_{t}=\overrightarrow{\mathrm{cumsum}}\left(\operatorname{softmax}\left(W_{\dot{f}} x_{t}+U_{\tilde{f}} h_{t-1}+b_{\tilde{f}}\right)\right) $
Forget gate: controls what is kept vs forgotten, from previous cell state
$\hat{f}_{t}=f_{t} \circ \omega_{t}+\left(\tilde{f}_{t}-\omega_{t}\right)=\tilde{f}_{t} \circ\left(f_{t} \circ \tilde{i}_{t}+1-\tilde{i}_{t}\right)$
Master Input gate: Ordered Input Gate Control Mechanism
$\tilde{i}_{t}=\overleftarrow{\mathrm{cumsum}}\left(\operatorname{softmax}\left(W_{\tilde{i}} x_{t}+U_{\tilde{i}} h_{t-1}+b_{\tilde{i}}\right)\right) =1-
\overrightarrow{\mathrm{cumsum}}\left(\operatorname{softmax}\left(W_{\tilde{i}} x_{t}+U_{\tilde{i}} h_{t-1}+b_{\tilde{i}}\right)\right)$
Input gate: controls what parts of the new cell content are written to cell
$\hat{i}_{t}=i_{t} \circ \omega_{t}+\left(\tilde{i}_{t}-\omega_{t}\right)=\tilde{i}_{t} \circ\left(i_{t} \circ \tilde{f}_{t}+1-\tilde{f}_{t}\right)$
Output gate: controls what parts of cell are output to hidden state
$\boldsymbol{o}^{(t)}=\sigma \left(\boldsymbol{W}_{o} \boldsymbol{h}^{(t-1)}+\boldsymbol{U}_{o} \boldsymbol{x}^{(t)}+\boldsymbol{b}_{o}\right)$
New cell content: this is the new content to be written to the cell
$\tilde{\boldsymbol{c}}^{(t)}=\tanh \left(\boldsymbol{W}_{c} \boldsymbol{h}^{(t-1)}+\boldsymbol{U}_{c} \boldsymbol{x}^{(t)}+\boldsymbol{b}_{c}\right)$
Cell state: erase (“forget”) some content from last cell state, and write (“input”) some new cell content
$c_{t}=\hat{f}_{t} \circ c_{t-1}+\hat{i}_{t} \circ \hat{c}_{t}$
Hidden state: read (“output”) some content from the cell
$\boldsymbol{h}^{(t)}=\boldsymbol{o}^{(t)} \circ \tanh \boldsymbol{c}^{(t)}$
 |
| ON-LSTM, Source: https://kexue.fm/archives/6621/comment-page-1 |
What's Next?
- Is "cumax"(cusum + softmax) really necessary?
From what I have observed., in reality the forget and input gates are not in the (0,0,0,1,1,1) or (1,1,1,0,0,0) regime. Take one for example:
[0.3182306 , 0.4296763 , 0.5659539 , 0.6581644 , 0.8738386 ,
0.94163144, 0.9522468 , 0.95804715, 0.960161 , 0.96124136,
0.96252906, 0.963744 , 0.964411 , 0.96599156, 0.9674326 ,
0.9684573 , 0.96898276, 0.9697275 , 0.97011393, 0.9703722 ,
0.9713492 , 0.9736657 , 0.97405773, 0.9745897 , 0.9753741 ,
0.97613144, 0.9766177 , 0.97877145, 0.98247737, 0.9835741 ,
0.9863124 , 0.9878812 , 0.9899598 , 0.9946286 , 0.99710023,
0.99824625, 0.9990951 , 0.9997795 , 0.99986076, 1.0000001 ]
This is not idealized version of gates. Too many of "middle states", limiting the ordering ability of ON-LSTM. It's possible to use softmax to assign to splitting point, but that leads to non-differentiability. - Is the hidden states in LSTM ordered?
Only cell states are ordered.
Reference:
Reference: